GPU 2D Drawing Part 2: Rectangle SDF. Masking. Rotations.
We also cover deriving rounded corners, inner shadow and line segments.
This is part of a series of hands-on tutorials. To get the most value, follow along and do your own experiments on shadertoy. I will not be sharing copy-pasteable snippets; only screenshots from shadertoy.
In the previous installment, we talked about the basics of SDF, what it means, and how we can use it to draw 2D shapes. We used the cricle as the basic shape to explore the concept. In this installment, we’ll talk about rectangles, masking and rotations.
Here’s the answer to the homework from the previous installment.
Rectangles
We can define rectangles in many ways: some people prefer (top_left, size) others prefer (top_left, bottom_right).
For SDF purposes, it's simpler to define rectangles with (center, half_size), just like we did with circles and borders.
Then there are 4 quadrants but they are all symmetric, so we can just consider one quadrant.
Remember what we want to compute: the distance between the point and the closest edge of the shape. It’s not enough to merely know whether the point is inside or outside the shape. We need its distance!
Unlike the circle, this shape is not so uniform. I placed several dots on the picture to illustrate all the cases I could think of:
Point inside, closer to the side edge (dark green dot).
Point inside, closer to the top edge (yellow dot).
Point outside, closer to the side edge (page dot).
Point outside, closer to the top edge (green dot).
Point outside, closer to the corner point (purple dot).
So we have three distances to consider: the signed distance to the side edge, the signed distance to the top edge, and the signed distance to the corner point (but we only want it for points outside the shape).
The distances to the side and top edge are not difficult to work out. It’s basically the same kind of computation we did for the circle’s radius.
// signed distance to the side edge
float x_dist = half_size.x - (point.x - center.x);
// signed distance to the top edge
float y_dist = half_size.y - (point.y - center.y;
// distance to corner (only valid for points outside the rectangle)
float c_dist = length(point - (center + half_size));Don’t take my word for it! Grab a pencil and paper and do your own sketches and make sure you can derive this calculation yourself.
Now, if we didn’t have the corner case, we could just take the maximum of x_dist and y_dist and be done!
It covers all the cases except the corner case where we need the distance to the corner point.
Here’s a picture to help visualize the situation. Other than the purple point, for each point the correct answer is equivalent to max(x_dist, y_dist)
Again do your own sketches to confirm this. Don’t take my word for it! At least, stare at the above illustration long enough to make sure you understand what it’s trying to convey.
The purple point happens to also be the only one with the property that both x_dist and y_dist are positve, so we can use this as the condition to select c_dist as the right answer.
Now remember, we are only considering one quadrant of the rectangle! The way I computed c_dist only applies to the top-right quadrant.
But remember: all the quadrants are symmetric.
Instead of littering the code with checks to see which quadrant we’re in, we can keep things simple by “normalize” the computations so that the center of the rectangle is always (0, 0), and then we take the absolute value for both the x and y axis of the point.
Think about it, if the rectangle’s center is at (0, 0), then the signed distance for the point (6, 5) is the same as the one for (-6, -5) and (-6, 5) and (6, -5).
Again, don’t take my word for it, do your own sketching and reasoning!
In the shader code we can calls abs(point) to return a point where all components are positive.
Now we can implement the function for the rectangle’s signed distance field.
And, it works!
Now, there’s a dramatic result that also appears. We have rounded corners for free! Where are they you say? Just watch.
If you’ve been paying attention very closely, you might have noticed that for points whose distance to the rect is measured by their distance to the corner point basically form a quadrant of a circle.
I will demonstrate this to you by drawing the border around the rect.
If you don’t understand why this is happening, go back to your pen and paper and make sure you understand the implications for how we computed the distance for the outer point with c_dist.
Growing and Shrinking Shapes
In the previous installment, we saw how to derive a “border” sdf from a regular sdf. Now let’s try to derive an sdf that represents a “growing” or a “shrinking” of the shape.
This will helps draw a rectangle with rounded corners. We just take a regular rectangle, then we grow it by x amount of pixels.
It’s actually quite simple: if a point has sdf value of 3 and we would like it to be the new edge, all we have to is subtract 3 from it. This applies to all points. If we subtract 3, the result is an sdf for a shape that is enlarged by 3 pixels. If we add 3, the result is an sdf for a shape that is shrunk by 3 pixels.
Now this gives us a way to draw a rectangle with rounded corners, but all the corners have the same radius. There are sdf functions out there that allows you to draw reactangles with different radius value for different corners. That might be interesting to explore, but I’m personally satisfied with what we have.
More importantly: I can derive it and understand how it works. This is infinitely more valuable than having something that does slightly more work but is undecipherable for me.
Instead of trying to come up with more and more shapes, I want to explore what operations can we do on shapes so that can we compose them in novel ways.
Two things come to my mind: masking (clipping) and rotations.
Clipping
Let’s say I want to draw a button with a “highlight” inside it. I can draw a highlight by drawing a blurry white-ish circle. But it’s not good if the circle spills outside the rectangle.
I want to only draw the pixels from the circle that also fit inside the rectangle.
Remember what we did with color filling a shape? We take the result value from the call to fill_factor, and then “applied” it to the front color by calling apply_factor.
If you think about it, this essentially clips the screen so that only the shape is visible.
If we also do the fill_factor and apply_factor calls for another shape, we essentially get the intersection of these two shapes.
Pause for a moment to think about this and make sure you understand what I’m saying.
Now, for demonstration, let’s start witha highlight effect that spills outside the rectangle
And now, with only a small change, we can clip the highlight inside the rect.
Watch this. Instead of just `apply_factor(hl_color, hl_f)` we’re going to apply both hl_f and rect_f.
It works! This makes me want to rename these functions. fill_factor → fill_mask and apply_factor → apply_mask
And we can do more! For the clipping shape, we can shrink the rectangle a little bit so that we have an inner border, and so that the highlight is really inside.
You can consider the above image a kind of optional homework. I’m not highlighting anything in the code sample. Here’s what I’d suggest you to do: try to create something similar on your own. If you are stuck anywhere, you may reference the code.
Rotations
Rotating points in 2D space is a topic in linear algebra. We can analyze the operation and derive the math for it, but I feel this is outside the scope of this tutorial. Instead we’ll just take the result, which is that we can construct a rotation matrix to rotate a point around the origin (0, 0) by an angle theta in the following way:
Which in shader code can be done this way:
float s = sin(a);
float c = cos(a);
mat2 m = mat2(c, -s, s, c)To rotate around a “pivot” point other than the origin, we first subtract our point from the pivot point, multiply with the rotation matrix, then add the pivot point back.
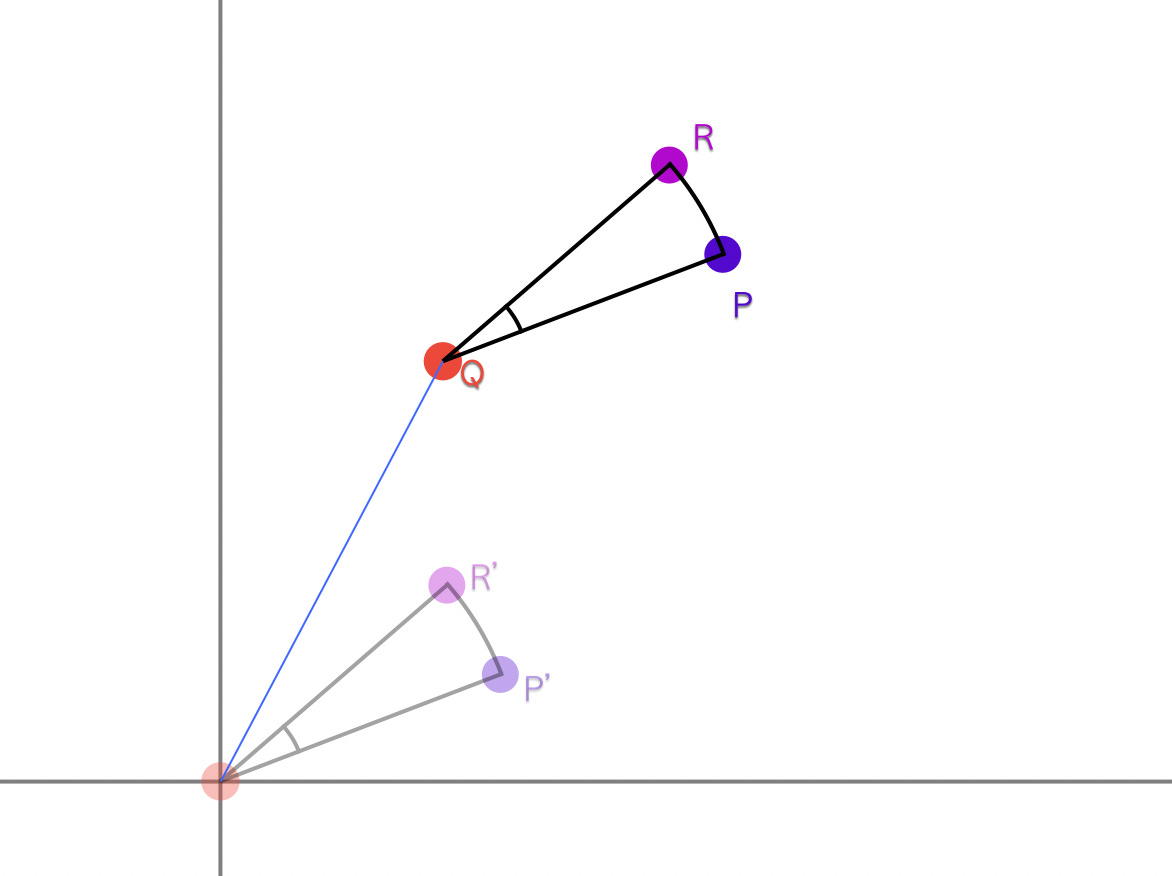
The diagram is an attempt to illustrate the reasoning. We have a point P that we want to rotate around Q to get the result R. But the matrix rotation M only rotates around the origin, so imagine we have the point P’ that we rotate around the origin (by multiplying with M) to get R’.
What is P’? It’s equivalent to the vector that goes from Q to P, and the same is true for R.
How do we apply rotations to shader code?
Remember, in shader code, we are deciding the color for the current point by getting the signed distance value for this point with respect to a given shape.
What if we want to rotate the shape? Then all points in space relative to it would be “rotated” in the same way, relative to where they would have been if the shape was not rotated.
So really, all we have to do is, rotate the current point we’re considering in the shader function, and that will produce a rotated shape!
In fact, the image above was generated by a little bit of shader code on shader toy.
I created some helper shape_xxx functions, but the relevant bit here is the rotation code, which I’ve highlighted.
If I comment out the `point = rotate_around(…)` line, I get the unrotated image (the left side image). If I keep that line, I get the rotated image (the right side image).
Line Segments
We can combine rectangles and rotations to derive the computation for the distance field of a line segment.
Generally speaking, a line segment is equivalent to a very thin rectangle rotated by some angle.
We don’t even need to derive the angle itself, because to apply the rotation we need the sin and cosine, and these are easy to derive from two points.
The diagram above illustrates the following point: we can draw the line from p1 to p2 by drawing another line first, from p1 to p2’ and then rotating it by the proper angle.
The rotation calculation uses the sin and cosine of the angle, so we don’t need to compute the angle per se. We just need the sign and the cosine. Those are defined in simple terms:
We can refactor the rotation logic to extract a function that takes just the sin and cosine, and then we have all the information we need!
It should be pretty obvious how to compute the other parameters. Take a few moments to make sure you can derive the computation yourself before you look at the code I’m going to provide.
The screenshot below shows a line drawn from the center of the rectangle to its halfsize corner point. You may notice it doesn’t go all the way to the rounded corner, but that’s because the rounded corner was gained by additionally “growing” sdf.
Now, this might be a very round about way of computing the signed distance field for a line segment. But it works.
And this is kind of the point of this exercise: to get a “base” of a building blocks that can be combined to create more intresting effects.
Inverse
A very simple shape transformation we can do is “inversion” of shapes. We take the distance from the sdf function and put a minus sign in front of it.
When combined with clipping, this allows us to do the inverse of clipping example we saw before.
We can also use it for inner shadow/highlights:
This will be the homework for this tutorial. The answer will be given at the start of the next tutorial.
Summary
We looked at the concept of a signed distance field for a shape, we looked at how to apply simple transformations to the shape, such as growing, bordering and inversion. We looked at how we can get a fill mask and use it to render the shape, we saw how can we can perform operations like blurring and rotation, and we saw how to apply multiple masks at the same time.
We also saw how we can combine these ideas to create some interesting result.
Keep in mind that we’re not interested in SDF for pure mathematical pleasure. We started down this path because we want to build a GUI toolkit that uses the GPU for rendering.
The are other components to a GUI library; namely: text rendering and layout. We’ll get to that later. One step at a time!
In my view, one of the reasons that web technology (html/css/js) became the defacto standard GUI toolkit is the flexibility it affords in terms of allowing people to create interesting visuals out of relatively simple building blocks. Most other UI toolkits only give you a set of “plain” standard widgets, and require you to write custom painting code if you want anything more interesting.
Any GUI toolkit, in order to be viable, has to be better than the web at affording this kind of flexibility.
In the next set of tutorials, we’ll start working on this toolkit to make it a reality. Our goal is to create a usable API that lets users create interesting layouts and interesting widgets with interesting interactions, not too different to what we would find in “rich” web application. Even better than them.
See you next time.